无约束优化的梯度方法
- 无约束优化的梯度方法
无约束优化的梯度方法
本文主要参照Princeton Prof. Yunxin Chen的Slides以及课堂笔记做的总结,聊一下无约束问题的梯度优化方法。既然提到了梯度,那么讨论的目标函数一定是可微的(可以用任意点处的的切平面来近似该点处的函数曲面)。后面有时间还会写一下约束优化问题的梯度方法,以及针对不可微目标函数的次梯度方法。
这篇文章真的超长,超出我的预期,后面改公式改到眼花。下次要分开写。
先来介绍几个基本概念:下降方向,迭代下降算法,以及大名鼎鼎的梯度下降。
-
下降方向 decent direction: 对于函数在$x$处沿$d$的方向导数
\[f'(x;d):=lim_{\tau \rightarrow 0} \frac{f(x+\tau d)-f(x)}{\tau} = \nabla f(x)^{\top} d,\]如果$d$满足方向导数$f’(x;d)=\nabla f(x)^{\top} d <0$, 那么称$d$为下降方向。
-
迭代下降算法 iterative descent algorithms: 从点$x^0$开始,构造序列${x^t}$,使得
\[f(x^{t+1})<f(x^{t}), t=0,1,...\]在每次迭代中,寻找在当前 $x^t$ 点的下降方向 $d^t$ , $x^{t+1} = x^{t} + \eta_{t} \nabla d^t$, 其中 $\eta_{t} >0$ 为步长。
-
梯度下降 Gradient Descent: $x^{t+1} = x^{t}-\eta_{t} \nabla f(x^t)$, 下降方向 $d^t=-\nabla f(x^t)$, 即最陡峭的下降方向,由Cauchy-Schwarz不等式
\[\arg \min_{d:\|d\|_2\le1}f'(x;d)= \arg \min_{\|d\|_2\le1}\nabla f(x)^{\top}d=-\frac{\nabla f(x)}{\|\nabla f(x)\|_2}\]
下面由特殊到一般,讨论一下各类无约束优化问题的下降算法及其收敛速度。
二次优化问题 Quadratic minimization problems
\[\min_x f(x):=\frac{1}{2} (x-x^*)^{\top}Q(x-x^*)\]其中 $Q\succ0, Q\in \mathbb{R}^{n\times n}$. $\nabla f(x)=Q(x-x^*)$.
该二次优化问题的解析解很容易看出
\[x = {x}^{*}, f({x}^{*})=0.\]这里讨论仅是验证梯度下降方法的收敛性。
常数步长及其收敛性
当每次迭代步长为固定值时,应该如何确定每次步长的大小呢? 最优选择为$\eta_t = \eta=\frac{2}{\lambda_1(Q)+\lambda_n(Q)}$, 此时有
\[\|x^t-x^*\|_2\le \left(\frac{\lambda_1(Q)-\lambda_n(Q)}{\lambda_1(Q)+\lambda_n(Q)}\right)^t \|x^0-x^*\|_2\]-
下面的证明会看到,选取步长使得
\[|1-\eta \lambda_{n} (Q)|=|1-\eta \lambda_{1} (Q)|\] - 收敛速度取决于 $Q$ 的 condition number $\frac{\lambda_{1}(Q)}{\lambda_{n}(Q)}$,即 $\frac{\max_{x}{\lambda_{1}(\nabla^{2} f(x))}}{\min_{x}{\lambda_{n}(\nabla^{2} f(x))}}$。
-
该收敛速度称为线性收敛 linear convergence 或几何收敛 geometric convergence. 这是因为 log(1/误差)和迭代次数 t 成线性关系,系数是 log(1/$\alpha$), $\alpha$为 $\frac{\lambda_{1}(Q)-\lambda_{n}(Q)}{\lambda_{1}(Q)+\lambda_{n}(Q)}$。
\[t log\left(\frac{1}{\alpha}\right)=log\left(\frac{\|x^0-x^*\|_{2}}{\epsilon}\right)\] -
Analysis: 想比较每次迭代后得到的结果和最优解的距离,先带入第t+1次GD迭代rule,
\[x^{t+1}-x^{*}=x^{t}-x^{*}-\eta_{t} \nabla f\left(x^{t}\right)=\left(\boldsymbol{I}-\eta_{t} \boldsymbol{Q}\right)\left(\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right)\]由Cauchy-Schwarz不等式得到此次距离和上次距离的关系,一个upper bound:
\[\left\|x^{t+1}-x^{*}\right\|_{2} \leq\left\|\boldsymbol{I}-\eta_{t} \boldsymbol{Q}\right\|\left\|\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right\|_{2}.\]现在要做的事情就是找到最优的 $\eta_t$ 使得每一步迭代都尽可能使得下一步距离更接近, 即最小化谱范数 $|\boldsymbol{I}-\eta \boldsymbol{Q}|$。 假如已经知道$Q$的特征值 $\lambda_1\ge…\ge\lambda_n\ge0$, 那么$\boldsymbol{I}-\eta \boldsymbol{Q}$的特征值$1-\eta\lambda_1\le…\le1-\eta\lambda_n$, 但如果没有具体例子,无法判断哪一个绝对值最大。 但是谱范数找的是绝对值最大的特征值的绝对值,因此可以确定
\[\|\boldsymbol{I}-\eta \boldsymbol{Q}\|=\max \left\{\left|1-\eta_{t} \lambda_{1}(\boldsymbol{Q})\right|,\left|1-\eta_{t} \lambda_{n}(\boldsymbol{Q})\right|\right\}\]那么由此我们有
\[\eta = \arg\min \max \left\{\left|1-\eta_{t} \lambda_{1}(\boldsymbol{Q})\right|,\left|1-\eta_{t} \lambda_{n}(\boldsymbol{Q})\right|\right\} =\frac{2}{\lambda_{1}(Q)+\lambda_{n}(Q)}\]此时
\[\|I-\eta Q\|=1-\frac{2 \lambda_{n}(\boldsymbol{Q})}{\lambda_{1}(\boldsymbol{Q})+\lambda_{n}(\boldsymbol{Q})}=\frac{\lambda_{1}(\boldsymbol{Q})-\lambda_{n}(\boldsymbol{Q})}{\lambda_{1}(\boldsymbol{Q})+\lambda_{n}(\boldsymbol{Q})}\]最后解释$\eta$的最优解如何求到的: 根据$\left|1-\eta_{t} \lambda_{1}(\boldsymbol{Q})\right|,\left|1-\eta_{t} \lambda_{n}(\boldsymbol{Q})\right|$的大小关系对$\eta$的取值和目标函数的取值进行分类讨论,
- 最小的特征值大于等于0: $0 \leq 1-\eta \lambda_{1}\Rightarrow \eta \leq \frac{1}{\lambda_{1}}$, 此时$|\boldsymbol{I}-\eta \boldsymbol{Q}|=\left|1-\eta_{t} \lambda_{n}(\boldsymbol{Q})\right|\geqslant \frac{\lambda_{1}-\lambda_{n}}{\lambda_{1}}$
- 最大的特征值小于等于0: $1- \lambda_{n} \leq 0 \Rightarrow \eta \geqslant \frac{1} {\lambda_{n}}$,此时$|\boldsymbol{I}-\eta \boldsymbol{Q}|=\left|1-\eta_{t} \lambda_{1}(\boldsymbol{Q})\right|\geqslant \frac{\lambda_{1}-\lambda_{n}}{\lambda_{1}}$
- 最小的小于0,最大的大于0: $1-\eta \lambda_{1}<0, \; 1-\eta \lambda_{n}>0 \Rightarrow \frac{1} {\lambda_{1}} \leqslant\eta \leqslant \frac{1}{\lambda_{n}}$. 该情况又分为两种: $\frac{1} {\lambda_{1}} <\eta \leqslant \frac{2}{\lambda_1+\lambda_{n}}$, 和 $\frac{2} {\lambda_{1}+\lambda_n} \leqslant\eta < \frac{1}{\lambda_{n}}$,最终可得$\eta = \frac{2} {\lambda_{1}+\lambda_n}$时 $|\boldsymbol{I}-\eta \boldsymbol{Q}|$取到最小 $\frac{\lambda_{1}(\boldsymbol{Q})-\lambda_{n}(\boldsymbol{Q})}{\lambda_{1}(\boldsymbol{Q})+\lambda_{n}(\boldsymbol{Q})}$。 这也是三种情况中的最小情况。
一种非固定的步长取值:Exact Line Search
上面讨论的是固定迭代步长 $\eta_t = \eta=\frac{2}{\lambda_1(Q)+\lambda_n(Q)}$ 的情况,但需要已知$Q$的谱特性。另一个更加practical的策略是 exact line search rule
\[\eta_{t}=\arg \min _{\eta \geq 0} f\left(\boldsymbol{x}^{t}-\eta \nabla f\left(\boldsymbol{x}^{t}\right)\right)\]目的是每一步迭代中,都选使得目标函数最小的那个步长。 该方法的收敛速度为
\[f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right) \leq\left(\frac{\lambda_{1}(\boldsymbol{Q})-\lambda_{n}(\boldsymbol{Q})}{\lambda_{1}(\boldsymbol{Q})+\lambda_{n}(\boldsymbol{Q})}\right)^{2 t}\left(f\left(\boldsymbol{x}^{0}\right)-f\left(\boldsymbol{x}^{*}\right)\right)\]- 与常数步长的收敛分析不同,此处用目标值说明收敛速度。
- 收敛速度为线性收敛 linear convergence,和常数步长的情况相似。
-
Analysis: 为方便,设 $\boldsymbol{g}^{t}=\nabla f\left(\boldsymbol{x}^{t}\right)=\boldsymbol{Q}\left(\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right)$,根据 exact line search rule 可以得到 $\eta_{t}=\frac{\boldsymbol{g}^{t \top} \boldsymbol{g}^{t}}{\boldsymbol{g}^{t^{\top}} \boldsymbol{Q} \boldsymbol{g}^{t}}$. 代入第 t+1 次的结果,找出与第 t 次的关系:
\[\begin{aligned} f\left(\boldsymbol{x}^{t+1}\right) &=\frac{1}{2}\left(\boldsymbol{x}^{t}-\eta_{t} \boldsymbol{g}^{t}-\boldsymbol{x}^{*}\right)^{\top} \boldsymbol{Q}\left(\boldsymbol{x}^{t}-\eta_{t} \boldsymbol{g}^{t}-\boldsymbol{x}^{*}\right) \\ &=\frac{1}{2}\left(\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right)^{\top} \boldsymbol{Q}\left(\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right)-\eta_{t}\left\|\boldsymbol{g}^{t}\right\|_{2}^{2}+\frac{\eta_{t}^{2}}{2} \boldsymbol{g}^{t \top} \boldsymbol{Q} \boldsymbol{g}^{t} \\ &=\frac{1}{2}\left(\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right)^{\top} \boldsymbol{Q}\left(\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right)-\frac{\left\|\boldsymbol{g}^{t}\right\|_{2}^{4}}{2 \boldsymbol{g}^{t \top} \boldsymbol{Q} \boldsymbol{g}^{t}} \\ &=\left(1-\frac{\left\|\boldsymbol{g}^{t}\right\|_{2}^{4}}{\left(\boldsymbol{g}^{t \top} \boldsymbol{Q} \boldsymbol{g}^{t}\right)\left(\boldsymbol{g}^{t \top} \boldsymbol{Q}^{-1} \boldsymbol{g}^{t}\right)}\right) f\left(\boldsymbol{x}^{t}\right) \end{aligned}\]最后一个等号用到了
\[f\left(x^{t}\right)=\frac{1}{2}\left(x^{t}-x^{*}\right)^{\top} Q\left(x^{t}-x^{*}\right)=\frac{1}{2} g^{t \top} Q^{-1} g^{t}.\]由 Kantorovich 不等式 (下降方法收敛性研究的核心)
\[\frac{\|\boldsymbol{y}\|_{2}^{4}}{\left(\boldsymbol{y}^{\top} \boldsymbol{Q} \boldsymbol{y}\right)\left(\boldsymbol{y}^{\top} \boldsymbol{Q}^{-1} \boldsymbol{y}\right)} \geq \frac{4 \lambda_{1}(\boldsymbol{Q}) \lambda_{n}(\boldsymbol{Q})}{\left(\lambda_{1}(\boldsymbol{Q})+\lambda_{n}(\boldsymbol{Q})\right)^{2}},\]代入得到
\[\begin{aligned} f\left(\boldsymbol{x}^{t+1}\right) & \leq\left(1-\frac{4 \lambda_{1}(\boldsymbol{Q}) \lambda_{n}(\boldsymbol{Q})}{\left(\lambda_{1}(\boldsymbol{Q})+\lambda_{n}(\boldsymbol{Q})\right)^{2}}\right) f\left(\boldsymbol{x}^{t}\right) \\ &=\left(\frac{\lambda_{1}(\boldsymbol{Q})-\lambda_{n}(\boldsymbol{Q})}{\lambda_{1}(\boldsymbol{Q})+\lambda_{n}(\boldsymbol{Q})}\right)^{2} f\left(\boldsymbol{x}^{t}\right) \end{aligned}\]
由于已知 $f\left(\boldsymbol{x}^{*}\right)=\min _{\boldsymbol{x}} f(\boldsymbol{x})=0$,收敛性得证。
强凸且光滑的问题 Strongly Convex and Smooth Problems
上面讨论了二次优化问题在梯度下降的情况,下面讨论稍一般的问题,目标函数为强凸且光滑的情况。强凸和光滑的定义及其等价定义后面有时间会写!!!!!!。对于一个二次可微 twice-differenctiable 的函数,$\mu$-strongly convex 且 $L$-smooth 如果满足
\[\mathbf{0} \preceq \mu \boldsymbol{I} \preceq \nabla^{2} f(\boldsymbol{x}) \preceq L \boldsymbol{I}, \quad \forall \boldsymbol{x}\]常数步长的情况
Theorem 1 (GD for strongly convex and smooth functions, constant stepsize) $f$ is $\mu$-strongly convex and $L$-smooth. If $\eta_{t} \equiv \eta=\frac{2}{\mu+L}$, then
\[\left\|x^{t}-x^{*}\right\|_{2} \leq\left(\frac{\kappa-1}{\kappa+1}\right)^{t}\left\|x^{0}-x^{*}\right\|_{2}\]where $\kappa :=L / \mu$ is condition number; $x^*$ is minimizer.
- 与二次函数情况的对比,步长 $\eta=\frac{2}{\mu+L}$ V.S. $\eta=\frac{2}{\lambda_{1}(\boldsymbol{Q})+\lambda_{n}(\boldsymbol{Q})}$; 收缩比例 $\frac{\kappa-1}{\kappa+1}$ V.S. $\frac{\lambda_{1}(Q)-\lambda_{n}(Q)}{\lambda_{1}(Q)+\lambda_{n}(Q)}$
- Dimension-free: 迭代复杂度为 $O\left(\frac{\log \frac{1}{\varepsilon}}{\log \frac{\kappa+1}{\kappa-1}}\right)$,与问题规模$n$无关,如果 $\kappa$ 不受 $n$ 的影响. 但是一般情况下,每次迭代的代价会受n影响,这样的话总的计算复杂度还是增加的。
- 依照smoothness的定义,以及 $\nabla f(x^*)=0$, 可得 \(f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right) \leq \frac{L}{2}\left(\frac{\kappa-1}{\kappa+1}\right)^{2 t}\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}^{2}\)
-
Analysis: 设
\[g(\tau)=f(x_\tau)=f(x^t+\tau(x^*-x^t))\]则
\[\int_0^1 g''(\tau)d\tau = g'(1)-g'(0)\]其中
\[\left\{x_{\tau}\right\}_{0 \leq \tau \leq 1}\]可看成是 $x^t$ 到 $x^*$ 间的线段.
Line Search 的情况:Backtracking Line Search
比起常数步长,实际中更常用 line search,现实中大多数用到的是 inexact line search,一个简单有效的方法是 backtracking line search. 不管哪一种步长选择,都是想用最小的代价尽可能快的找到最优点。Backingtracking line search 的思想是:在搜索方向上,先设置一个初始步长,如果过大则缩减步长,直到合适为止。这就涉及到如何判断步长是否合适、如果缩短步长两个问题。
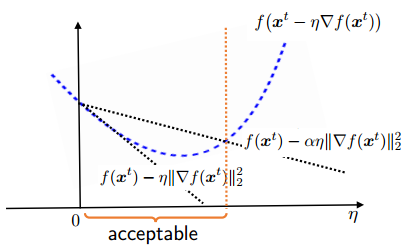
确保充分下降的 Armijo condition: 存在 $0< \alpha < 1$ 使得
\[f\left(\boldsymbol{x}^{t}-\eta \nabla f\left(\boldsymbol{x}^{t}\right)\right)<f\left(\boldsymbol{x}^{t}\right)-\alpha \eta\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}\](可以由泰勒公式展开得到) 但是!实际中我们选择的 $0< \alpha < \frac{1}{2}$,至于原因,是希望算法的收敛速度更快(下降速度更快),有人说和超线性收敛有关,具体参考《最优化理论与方法》(袁亚湘),我还没check。缩减的方法采用反复乘以一个小于1的系数 $\beta$ .

当初始步长足够大时,根据上述算法得到的步长 $\eta$ 具有 lower bound, 找到 $\eta$ 一个取值,使得当 $\eta = \tilde{\eta}_t$ 时,算法不会使 $\eta$ 减小,根据算法中步长的缩减规则,我们有
\[\eta_{t} \geq \beta \tilde{\eta}_{t}.\]这个值我们取目标迭代函数值的上限
\[f\left(\boldsymbol{x}^{t}\right)-\alpha \eta\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}\]与二阶近似的上限
\[f\left(\boldsymbol{x}^{t}\right)-\eta\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}+\frac{L \eta^{2}}{2}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}\]相等的根。 这里二阶近似的上限用到了目标函数的光滑性 $L$-smoothness. 这是因为对于光滑函数,当 $\eta = \tilde{\eta}_t$ 时,
\[f\left(\boldsymbol{x}^{t}-\eta \nabla f\left(\boldsymbol{x}^{t}\right)\right)\le f\left(\boldsymbol{x}^{t}\right)-\eta\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}+\frac{L \eta^{2}}{2}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}.\] \[\begin{array}{l}{f\left(\boldsymbol{x}^{t}\right)-\alpha \eta\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}=f\left(\boldsymbol{x}^{t}\right)-\eta\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}+\frac{L \eta^{2}}{2}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}} \\ {\Longrightarrow \quad \eta_{t} \geq \frac{2(1-\alpha) \beta}{L} = \tilde{\eta}_{t}}\end{array}\]实际中, backtracking line search 通常可以对局部 Lipschitz 常数 (local Lipschitz constant) $|\nabla f(x)- \nabla f(y)| \le L | x-y|$ 给出良好估计。 \(L \geq \frac{2(1-\alpha) \beta}{\eta_{t}}\)
Theorem 2 (GD for strongly convex and smooth functions, backtracking line search) $f$ is $\mu$-strongly convex and $L$-smooth. With backtracking line search,
\[f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right) \leq\left(1-\min \left\{2 \mu \alpha, \frac{2 \beta \alpha \mu}{L}\right\}\right)^{t}\left(f\left(\boldsymbol{x}^{0}\right)-f\left(\boldsymbol{x}^{*}\right)\right)\]where $x^*$ is minimizer.
和 constant stepsize 不同的是用目标函数值来表达收敛性,但同样是线性收敛 linear convergence.
线性收敛一定要求强凸吗?
上面我们讨论了在目标函数$\mu$-strongly convex 和 $L$-smooth 的情况下具有线性收敛性,那可否在不满足强凸的情况下也具备线性收敛呢?其实,强凸性可以被 relaxed 成
- 局部强凸性 local strong convexity
- 正则条件 regularity condition
- P-L 条件 Polyak-Lojasiewicz condition
局部强凸 Local strong convexity
这里举一个耳熟能详(并不)的栗子——逻辑回归 logistic regression.
逻辑回归 Logistic Regression
给定 $N$ 个独立样本,${x_i, g_i}_{i=1}^N$, 其中 $x_i \in \mathbb{R}^p$ 是已知的设计向量,$g_i \in {1, …, K}$ 是 $K$ 分类的结果,我们希望学习到给定设计向量判断分类的方法。这部分是背景,参考了 The Elements of Statistic Learning, Hastie et. al.
逻辑回归的思想是根据样本特征的线性函数来建模,得到属于各类别的后验概率,同时保证概率和为1、且每一种概率大小都在 $[0, 1]$ 范围内。我们让线性回归 $a^\top x + b_0$ (连续、无界)的值恰好为后验概率的 log 函数
\[\begin{aligned} \log \operatorname{Pr}(G=1 | X=x) &=\beta_{10}+\beta_{1}^{T} x \\ \log {\operatorname{Pr}(G=2 | X=x)} &=\beta_{20}+\beta_{2}^{T} x \\ & \vdots \\ \log {\operatorname{Pr}(G=K-1 | X=x)} &=\beta_{(K-1) 0}+\beta_{K-1}^{T} x \\ \log {\operatorname{Pr}(G=K | X=x)} &=\beta_{(K) 0}+\beta_{K}^{T} x \\ \sum_{k=1}^K \operatorname{Pr}(G=k | X=x) &= 1 \end{aligned}\]上面可以看成是 $K$ 组未知数 ${ \beta_{k0}, \beta_k }$, $K+1$ 个方程,把最后一个式子看成约束条件,就可以约去一个表达式(一旦其中 $K-1$ 组未知数确定,由约束条件亦可确定最后一组)。我们假设约去了第K个表达式,就得到
\[\begin{aligned} \log \frac{\operatorname{Pr}(G=1 | X=x)}{\operatorname{Pr}(G=K | X=x)} &=\beta_{10}+\beta_{1}^{T} x \\ \log \frac{\operatorname{Pr}(G=2 | X=x)}{\operatorname{Pr}(G=K | X=x)} &=\beta_{20}+\beta_{2}^{T} x \\ & \vdots \\ \log \frac{\operatorname{Pr}(G=K-1 | X=x)}{\operatorname{Pr}(G=K | X=x)} &=\beta_{(K-1) 0}+\beta_{K-1}^{T} x \end{aligned}\]上面 $K-1$ 个式子暗含了约束条件:概率和为1. 求个exp加起来加个1除一除乘一乘就可以得到
\[\begin{aligned} \operatorname{Pr}(G=k | X=x) &= \frac{\exp \left(\beta_{k 0}+\beta_{k}^{T} x\right)}{1+\sum_{\ell=1}^{K-1} \exp \left(\beta_{\ell 0}+\beta_{\ell}^{T} x\right)}, k=1, \ldots, K-1 \\ \operatorname{Pr}(G=K | X=x) &= \frac{1}{1+\sum_{\ell=1}^{K-1} \exp \left(\beta_{\ell 0}+\beta_{\ell}^{T} x\right)} \end{aligned}\]上面的式子明显和为1. 我们将参数集合表示为
\[\theta=\left\{\beta_{10}, \beta_{1}^{T}, \ldots, \beta_{(K-1) 0}, \beta_{K-1}^{T}\right\}.\]为了强调对参数集的 dependence,将概率表示为
\[\operatorname{Pr}(G=k | X=x)=p_{k}(x ; \theta).\]当 $K=2$ 时,上述式子只有一个,是最简单但是非常常用的情况。 现在已经有了模型,接下来要做的就是,利用观察到的样本们去学习 fit 它! 也就是根据样本、目标函数 fit 参数集合 $\theta$. 如何习得参数们呢?逻辑回归通常采用的是最大似然(参数估计的一种方法,基础概率还要补一补,何况是测度blabla…后面有时间会写的)去fit——用给定 $X$ 时 $G$ 的条件似然。 由于 $\operatorname{Pr}(G | X)$ 完全确定了条件分布,多项分布 multinomial distribution 是合适的(应该是well defined的意思)。
现在假设有 $N$ 个独立样本,
\[\{x_i, g_i\}_{i=1}^N,\]其中 $x_i$ 是已知的设计向量,$g_i$ 是 $K$ 分类的结果。根据前面的分析,设这些样本服从前面的条件分布:
\[\{p_{k}(x ; \theta)\}_{k=1}^K.\]我们希望:找到一组参数 $\theta$ 使得观察到的样本出现的概率最大。 这个概率的表达式为
\[p\left(x_{1}, \dots, x_{N} ; \theta\right) = \prod_{i=1}^{N} p_{g_i}\left(x_{i} ; \theta \right)\]最大化这个概率等价于最大化这个概率的log函数,所求的变量自然是参数集合 $\theta$. 因此可以写成 $\theta$ 的函数
\[\ell(\theta)=\sum_{i=1}^{N} \log p_{g_{i}}\left(x_{i} ; \theta\right)\]其中
\[p_{k}{\left( x_{i} ; \theta \right)} = \operatorname{Pr} {\left(G=k | X=x_{i} ;\theta \right)}.\]下面我们详细讨论一下二分类的情况,这种情况下算法会大大简化。将两种类别 $g_i$ 编码为取值 ${0,1}$ 的响应 $y_i$, 当 $g_{i}=1$ 时,取 $y_{i}=1$,当 $g_{i}=2$ 时取 $y_{i}=0$. 并让 $p_{1}(x ; \theta)=p(x ; \theta)$,则 $p_{2}(x ; \theta)=1-p(x ; \theta)$. 那么,对于某个样本而言,就实现了log表达式的统一:
- 若样本类别为 $y_i = 1$,则 $\log p_{y_i}(x ; \theta) = \log p(x ; \beta) = y_i \log p(x ; \beta) + (1-y_i) \log \left(1-p(x ; \beta) \right)$,
- 若样本类别为 $y_i = 0$,则 $\log p_{y_i}(x ; \theta) = \log \left(1-p(x ; \beta) \right) = y_i \log p(x ; \beta) + (1-y_i) \log \left(1-p(x ; \beta) \right)$.
此时 log-likelihood 可写成关于参数 $\beta$ 的函数
\[\begin{aligned} \ell(\beta) &=\sum_{i=1}^{N}\left\{y_{i} \log p\left(x_{i} ; \beta\right)+\left(1-y_{i}\right) \log \left(1-p\left(x_{i} ; \beta\right)\right)\right\} \\ &=\sum_{i=1}^{N}\left\{y_{i} \log \frac {p\left(x_{i} ; \beta\right)}{1-p\left(x_{i} ; \beta\right)} + \log \left(1-p\left(x_{i} ; \beta\right)\right)\right\} \\ &=\sum_{i=1}^{N}\left\{y_{i} \beta^{T} x_{i}-\log \left(1+e^{\beta^{T} x_{i}}\right)\right\} \end{aligned}\]最后一个式子就是代入前面条件概率的表达式得到的,这里
\[\beta = \left\{ \beta_{10}, \beta_{1} \right\},\]并假设输入向量 $x_i \in {1 \times \mathbb{R}^p}$ 中已经包含了对应之前 $\beta_{10}$ 的常数项1.
到这里整个逻辑回归的数学模型就已经建立了,下面就是优化的部分了(其实优化部分才是本文重点)。之前看了一些关于逻辑回归的博客,甚至还做过project,但感觉理解不够透彻,有些原理在一些博客被忽略掉了,自己作为小白就会比较难受,现在根据《统计学习要素》中的讲解整理一下,思路就清晰许多。实际上关于逻辑回归有很多角度的解释,但自己感觉这个版本最清晰也最根本,有理有据。以后有新的视角也会补充进来。
为了最大化 log-likelihood,我们令其导数为0,
\[\frac{\partial \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}}=\sum_{i=1}^{N} \boldsymbol{x}_{i}\left(y_{i}-p\left(\boldsymbol{x}_{i} ; \boldsymbol{\beta}\right)\right)=\boldsymbol{0}\]这实际上是 $p+1$ 个关于 $\boldsymbol{\beta}$ 的非线性方程。 由于 $\boldsymbol{x}_i$ 的第一项为1,那么第一个非线性方程要求
\[\sum_{i=1}^{N} y_{i}=\sum_{i=1}^{N} p\left(\boldsymbol{x}_i ; \boldsymbol{\beta}\right)\]即观察到分类为1的样本数目与期望的分类为1的数目一致(分类为0的样本数目因此也是一致的)。 进一步求其 Hessian 矩阵,
\[\frac{\partial^{2} \ell(\beta)}{\partial \beta \partial \beta^{T}}=-\sum_{i=1}^{N} x_{i} x_{i}^{T} p\left(x_{i} ; \beta\right)\left(1-p\left(x_{i} ; \beta\right)\right)\]看到 Hessian 负定没关系,因为是最大化似然函数,所以加个负号变成minimize,Hessian 自然也是正定的。但这个只是一般情况!当 $x \rightarrow \infty$ 时,$p\left(x_{i} ; \beta\right)\left(1-p\left(x_{i} ; \beta\right)\right) = \frac{\exp \left( \beta^{\top} x_i \right)}{\left(1+\exp \left(\beta^{\top} x_i\right)\right)^{2}} \rightarrow 0$, 因此目标函数竟然是 0-strongly convex的,想不到吧。现在终于回到正题,目标函数难道不具备线性收敛性吗?
常数步长的线性收敛性
Theorem 3 (GD for locally strongly convex and smooth functions, constant stepsize) $f$ is locally $\mu$-strongly convex and $L$-smooth such that
\[\mu \boldsymbol{I} \preceq \nabla^{2} f(\boldsymbol{x}) \preceq L \boldsymbol{I}, \quad \forall \boldsymbol{x} \in \mathcal{B}_{0}\]where
\[\mathcal{B}_{0} :=\left\{\boldsymbol{x} :\left\|\boldsymbol{x}-\boldsymbol{x}^{*}\right\|_{2} \leq\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}\right\}.\]Then Theorem 1 continues to hold, i.e., if $\eta_{t} \equiv \eta=\frac{2}{\mu+L},$
then
\[\left\|x^{t}-x^{*}\right\|_{2} \leq\left(\frac{\kappa-1}{\kappa+1}\right)^{t}\left\|x^{0}-x^{*}\right\|_{2}\]where $\kappa :=L / \mu$ is condition number; $x^*$ is minimizer.
-
对任意 $x^{t} \in \mathcal{B}_{0}$, 可得
\[\left\|x^{t+1}-x^{*}\right\|_{2} \leq \frac{\kappa-1}{\kappa+1}\left\|x^{t}-x^{*}\right\|_{2}\]则有
\[\boldsymbol{x}^{t+1} \in \mathcal{B}_{0},\]因此上述上限将在后来的迭代中继续成立。
-
回到逻辑回归的例子,local strong convexity 的参数表达式为
\[\inf _{x :\left\|x-x^{*}\right\|_{2} \leq\left\|x^{0}-x^{*}\right\|_{2}} \lambda_{\min }\left( \sum_{i=1}^{N} \frac{\exp \left( \beta^{\top} x_i \right)}{\left(1+\exp \left(\beta^{\top} x_i\right)\right)^{2}} \boldsymbol{a}_{i} \boldsymbol{a}_{i}^{\top} \right)\]该表达式常常与0有严格距离,因此使得线性收敛性成立。
正则条件 Regularity condition
另一个可以替代强凸和光滑要求的是正则条件。
\[\left\langle\nabla f(\boldsymbol{x}), \boldsymbol{x}-\boldsymbol{x}^{*}\right\rangle \geq \frac{\mu}{2}\left\|\boldsymbol{x}-\boldsymbol{x}^{*}\right\|_{2}^{2}+\frac{1}{2 L}\|\nabla f(\boldsymbol{x})\|_{2}^{2}, \quad \forall \boldsymbol{x}\]它是这么得到的:
- L-smoothness: $\langle\nabla f(x)-\nabla f(y), x-y\rangle \leq M|x-y|_{2}^{2} \quad \forall x, y \in \mathbb{R}^{d}$
- $\mu$-convexity: $\langle\nabla f(x)-\nabla f(y), x-y\rangle \geq \mu |x-y|_{2}^{2} \quad \forall x, y \in \mathbb{R}^{d}$
-
上述两式相加,
\[y \rightarrow x^{*}\]代入
\[\nabla f(x^{*})=0\] - 强凸要求每一对 $(x,y)$ 都要满足条件,正则条件只要求了 $(x,x^*)$.
Theorem 4 (GD for functions satisfying regularity condition, constant stepsize) Suppose $f$ satisfies
\[\left\langle\nabla f(\boldsymbol{x}), \boldsymbol{x}-\boldsymbol{x}^{*}\right\rangle \geq \frac{\mu}{2}\left\|\boldsymbol{x}-\boldsymbol{x}^{*}\right\|_{2}^{2}+\frac{1}{2 L}\|\nabla f(\boldsymbol{x})\|_{2}^{2}, \quad \forall \boldsymbol{x}\]If $\eta_{t} \equiv \eta=\frac{1}{L}$, then
\[\left\|x^{t}-x^{*}\right\|_{2}^{2} \leq\left(1-\frac{\mu}{L}\right)^{t}\left\|x^{0}-x^{*}\right\|_{2}^{2}\]Proof.
\[\begin{aligned}\left\|x^{t+1}-x^{*}\right\|_{2}^{2} &=\left\|x^{t}-x^{*}-\frac{1}{L} \nabla f\left(x^{t}\right)\right\|_{2}^{2} \\ &=\left\|x^{t}-x^{*}\right\|_{2}^{2}+\frac{1}{L^{2}}\left\|\nabla f\left(x^{t}\right)\right\|_{2}^{2}-\frac{2}{L}\left\langle x^{t}-x^{*}, \nabla f\left(x^{t}\right)\right\rangle \\ & \leq\left\|x^{t}-x^{*}\right\|_{2}^{2}-\frac{\mu}{L}\left\|x^{t}-x^{*}\right\|_{2}^{2} \\ &=\left(1-\frac{\mu}{L}\right)\left\|x^{t}-x^{*}\right\|_{2}^{2} \end{aligned}\]其中不等式利用了regularity condition. $\; \blacksquare$
P-L 条件 Polyak-Lojasiewicz condition
存在 $\mu>0$ 使得
\[\|\nabla f(\boldsymbol{x})\|_{2}^{2} \geq 2 \mu\left(f(\boldsymbol{x})-f\left(\boldsymbol{x}^{*}\right)\right), \quad \forall \boldsymbol{x}\]- 强凸:$f(y)-f(x)-\langle\nabla f(x), y-x\rangle \leq \frac{1}{2 \mu}|\nabla f(x)-\nabla f(y)|_{2}^{2} \quad \forall x, y \in \mathbb{R}^{d}$. PL 条件: $y \rightarrow x, x \rightarrow x^*$. 强凸一定PL.
- 当远离最优目标值时,梯度上升速度加快。
- 每个驻点 stationary point (梯度为0的点)都是全局最优。
Theorem 5 (GD for functions satisfying smoothness and PL condition, constant stepsize) Suppose $f$ is $L$-smooth and satisfies
\[\|\nabla f(\boldsymbol{x})\|_{2}^{2} \geq 2 \mu\left(f(\boldsymbol{x})-f\left(\boldsymbol{x}^{*}\right)\right), \quad \forall \boldsymbol{x}\]If $\eta_{t} \equiv \eta=\frac{1}{L}$, then
\[f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right) \leq\left(1-\frac{\mu}{L}\right)^{t}\left(f\left(\boldsymbol{x}^{0}\right)-f\left(\boldsymbol{x}^{*}\right)\right)\]- 最优目标值的线性收敛性
- 未必有唯一全局最优解
- 证明在后面
例子:over-parametrized linear regression
给 n 个数据样本,${a_i \in \mathbb{R}^d, y_i\in \mathbb{R}}_{1\le i\le n}$ 进行线性回归,找到 fit 数据的最好的线性模型
\[\underset{x \in \mathbb{R}^{d}}{\operatorname{minimize}} f(x) \triangleq \frac{1}{2} \sum_{i=1}^{n}\left(a_{i}^{\top} x-y_{i}\right)^{2}\]over-parametrization: 模型的维度 $d$ $>$ 样本数量 $n$ 在深度学习中尤为重要。 该问题是凸的,但不是强凸的,因为
\[\nabla^{2} f(\boldsymbol{x})=\sum_{i=1}^{n} \boldsymbol{a}_{i} \boldsymbol{a}_{i}^{\top}\]当 $d>n$ 时不满秩。但大多数时候仍然满足 $f\left(\boldsymbol{x}^{*}\right)=0$ 以及 PL 条件,因此GD线性收敛。
Fact 1 Suppose that
\[\boldsymbol{A}=\left[\boldsymbol{a}_{1}, \cdots, \boldsymbol{a}_{n}\right]^{\top} \in \mathbb{R}^{n \times d}\]has rank $n$, and that
\[\eta_{t} \equiv \eta=\frac{1}{\lambda_{\max }\left(A A^{\top}\right)}.\]Then GD obeys
\[f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right) \leq\left(1-\frac{\lambda_{\min}\left(\boldsymbol{A} \boldsymbol{A}^{\top}\right)}{\lambda_{\max}\left(\boldsymbol{A} \boldsymbol{A}^{\top}\right)}\right)^{t}\left(f\left(\boldsymbol{x}^{0}\right)-f\left(\boldsymbol{x}^{*}\right)\right), \quad \forall t\]-
原问题的 Hessian
\[\nabla^{2} f(\boldsymbol{x})=\sum_{i=1}^{n} \boldsymbol{a}_{i} \boldsymbol{a}_{i}^{\top} = \boldsymbol{A}^{\top} \boldsymbol{A}\in \mathbb{R}^{d\times d}\] - 对 ${ \boldsymbol{a}_{i}}$ 的假设温和
- 对 ${ y_{i}}$ 没有要求
- 当有很多全局最优解时,对该over-parametrized 问题,GD 给出的结果有偏好,往往收敛到距离初始化 $x^0$ 最近的全局最优。
-
证明:
$\boldsymbol{A}^{\top} \boldsymbol{A}$ 和 $\boldsymbol{A} \boldsymbol{A}^{\top}$ 的特征值除0外相同(可以用SVD证明), 因此最大的特征值相同。 由于在Over-Parametrized 问题中 $f\left(x^{*}\right) = 0$ 因此只需要证明 $\lambda_{\min}\left(A A^{\top}\right)$ 就是 PL 条件中的 $\mu$ 即可, 也就是
\[\|\nabla f(\boldsymbol{x})\|_{2}^{2} \geq 2 \lambda_{\min}\left(\boldsymbol{A} \boldsymbol{A}^{\top}\right) f(\boldsymbol{x}).\]如果该不等式成立,那么 Fact 1 得证。 下面就证明这个不等式。 令
\[\boldsymbol{y}=\left[y_{i}\right]_{1 \leq i \leq n},\]则
\[\boldsymbol{x}^{*}=\boldsymbol{x}-\boldsymbol{A}^{\top}\left(\boldsymbol{A} \boldsymbol{A}^{\top}\right)^{-1}(\boldsymbol{A} \boldsymbol{x}-\boldsymbol{y}) = \arg \min _{A z=y}\|z-x\|_{2}.\]我们有
\[\begin{aligned} \nabla f(\boldsymbol{x}) &=\sum_{i} \boldsymbol{a}_{i}\left(\boldsymbol{a}_{i}^{\top} \boldsymbol{x}-y_{i}\right)=\sum_{i} \boldsymbol{a}_{i}\left(\boldsymbol{a}_{i}^{\top} \boldsymbol{x}-\boldsymbol{a}_{i}^{\top} \boldsymbol{x}^{*}\right) \\ &=\left(\sum_{i} \boldsymbol{a}_{i} \boldsymbol{a}_{i}^{\top}\right)\left(\boldsymbol{x}-\boldsymbol{x}^{*}\right)=\boldsymbol{A}^{\top} \boldsymbol{A}\left(\boldsymbol{x}-\boldsymbol{x}^{*}\right) \\ &=\boldsymbol{A}^{\top} \boldsymbol{A} \boldsymbol{A}^{\top}\left(\boldsymbol{A} \boldsymbol{A}^{\top}\right)^{-1}(\boldsymbol{A} \boldsymbol{x}-\boldsymbol{y}) \quad \\ &=\boldsymbol{A}^{\top}(\boldsymbol{A} \boldsymbol{x}-\boldsymbol{y}) \end{aligned}\]
结果有
\[\begin{aligned} \|\nabla f(\boldsymbol{x})\|_{2}^{2} &=(\boldsymbol{A} \boldsymbol{x}-\boldsymbol{y})^{\top} \boldsymbol{A} \boldsymbol{A}^{\top}(\boldsymbol{A} \boldsymbol{x}-\boldsymbol{y}) \\ & \geq \lambda_{\min }\left(\boldsymbol{A} \boldsymbol{A}^{\top}\right)\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{y}\|_{2}^{2} \\ &=2 \lambda_{\min }\left(\boldsymbol{A} \boldsymbol{A}^{\top}\right) f(\boldsymbol{x}) \quad \blacksquare \end{aligned}\]凸且光滑的问题 Convex and smooth problems
没有强凸性时,研究收敛性往往用目标函数值
\[\| f(x^{t})-f(x^{*})\|\]的收敛而不是最优解
\[\|x^{t}-x^{*}\|\]的收敛。举个例子,函数
\[f(x)= \frac{1}{x} \; \; (x>0)\]GD 迭代下去很可能难以收敛到
\[x^{*}=\infty\]相比之下,
\[f(x^{t})\]可能很快达到
\[f \left( x^{*} \right) = 0\]保证目标函数下降吗
那么问题来了,不具备强凸性时,我们能保证目标函数值下降(i.e., $f\left(\boldsymbol{x}^{t+1}\right)<f\left(\boldsymbol{x}^{t}\right)$)吗?如何选择步长才能保证充分的下降呢? 关键思想: majorization-minimization, 给 $f(x)$ 找到简单的 majorizing function 然后优化这个替代函数。
由于光滑,
\[\begin{aligned} f\left(\boldsymbol{x}^{t+1}\right)-f\left(\boldsymbol{x}^{t}\right) & \leq \nabla f\left(\boldsymbol{x}^{t}\right)^{\top}\left(\boldsymbol{x}^{t+1}-\boldsymbol{x}^{t}\right)+\frac{L}{2}\left\|\boldsymbol{x}^{t+1}-\boldsymbol{x}^{t}\right\|_{2}^{2} \\ &=-\eta_{t}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}+\frac{\eta_{t}^{2} L}{2}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2} \end{aligned}\]最后一个等号后面的就是由光滑得到的目标函数下降的 majorizing function,我们想要最大化每次迭代的下降程度的下限,就要最大化
\[\left(\eta_{t}-\frac{\eta_{t}^{2} L}{2}\right)\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}\]选择 $\eta_{t}=1 / L$ 取到最大,此时每次迭代至少使目标函数下降
\[\frac{1}{2 L}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}\]我们就有了下面的 Fact 2.
Fact 2 Suppose $f$ is L-smooth. Then GD with $\eta_{t}=1 / L$ obeys
\[f\left(\boldsymbol{x}^{t+1}\right) \leq f\left(\boldsymbol{x}^{t}\right)-\frac{1}{2 L}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}\]- 当步长足够小时,GD可以保证目标函数值下降。因为:令下降值下限 $\left(\eta_{t}-\frac{\eta_{t}^{2} L}{2}\right)\left|\nabla f\left(\boldsymbol{x}^{t}\right)\right|_{2}^{2}>0$ 可得 $0<\eta_t<2/L$.
- 并不依赖凸性!
GD 不仅可以优化目标函数值,只要步长不太大,迭代时也会逐渐靠近最优解。将 $f$ 看作 0-strongly convex 可以根据前面的分析得到
\[\left\|x^{t+1}-x^{*}\right\|_{2} \leq\left\|x^{t}-x^{*}\right\|_{2}\]也就是说,$\left|x^{t}-x^{*}\right|_{2}$ 对 $t$ 单调不增.
实际上,可以进一步证明除非 $\boldsymbol{x}^{t}$ 已经是最优解,$\left|x^{t}-x^{*}\right|_{2}$ 是严格下降的。
Fact 3 Suppose $f$ is convex and L-smooth. If $\eta_{t}=1 / L$, then
\[\left\|x^{t+1}-x^{*}\right\|_{2} \leq\left\|x^{t}-x^{*}\right\|_{2}-\frac{1}{L^{2}}\left\|\nabla f\left(x^{t}\right)\right\|_{2}^{2}\]-
证明:
\[\begin{aligned} \left\|x^{t+1}-x^{*}\right\|_{2}^{2} &=\left\|x^{t}-x^{*}-\eta\left(\nabla f\left(x^{t}\right)-\nabla f\left(x^{*}\right)\right)\right\|_{2}^{2} \\ &=\left\|x^{t}-x^{*}\right\|_{2}^{2}-2 \eta\left\langle\boldsymbol{x}^{t}-\boldsymbol{x}^{*}, \nabla f\left(\boldsymbol{x}^{t}\right)-\nabla f\left(\boldsymbol{x}^{*}\right)\right\rangle+\eta^{2}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)-\nabla f\left(\boldsymbol{x}^{*}\right)\right\|_{2}^{2} \end{aligned}\]由于 smooth 且 convex,
\[\left\langle\boldsymbol{x}^{t}-\boldsymbol{x}^{*}, \nabla f\left(\boldsymbol{x}^{t}\right)-\nabla f\left(\boldsymbol{x}^{*}\right)\right\rangle \geq \frac{1}{L}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)-\nabla f\left(\boldsymbol{x}^{*}\right)\right\|_{2}^{2},\]又因为 $\eta_{t}=1 / L$, 我们有
\[\left\|x^{t+1}-x^{*}\right\|_{2}^{2}\leq\left\|\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right\|_{2}^{2}-\eta^{2}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)-\nabla f\left(\boldsymbol{x}^{*}\right)\right\|_{2}^{2},\]其中 $\nabla f\left(\boldsymbol{x}^{*}\right)=0$. $\blacksquare$
现在可以证明前面的 Theorem 5 了。回顾一下 Theorem 5 说了什么。
Theorem 5 (GD for functions satisfying smoothness and PL condition, constant stepsize) Suppose $f$ is $L$-smooth and satisfies
\[\|\nabla f(\boldsymbol{x})\|_{2}^{2} \geq 2 \mu\left(f(\boldsymbol{x})-f\left(\boldsymbol{x}^{*}\right)\right), \quad \forall \boldsymbol{x}\]If $\eta_{t} \equiv \eta=\frac{1}{L}$, then
\[f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right) \leq\left(1-\frac{\mu}{L}\right)^{t}\left(f\left(\boldsymbol{x}^{0}\right)-f\left(\boldsymbol{x}^{*}\right)\right)\]Proof.
\[\begin{aligned} f\left(\boldsymbol{x}^{t+1}\right)-f\left(\boldsymbol{x}^{*}\right) & \leq f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right)-\frac{1}{2 L}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2} \\ & \leq f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right)-\frac{\mu}{L}\left(f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right)\right) \\ &=\left(1-\frac{\mu}{L}\right)\left(f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right)\right) \end{aligned}\]收敛性分析
不幸的是,没有强凸性时,收敛速度将远远慢于线性收敛(或几何收敛)。
Theorem 6 (GD for convex and smooth problems) Let $f$ be convex and $L$-smooth. If $\eta_{t} \equiv \eta=1 / L$, then GD obeys
\[f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right) \leq \frac{2 L\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}^{2}}{t}\]- 要达到 $\epsilon$-准确,需要 $O(1/\epsilon)$ 次迭代。线性收敛: $O(\log{\frac{1}{\epsilon}})$.
-
证明: 由 Fact 2,
\[f\left(\boldsymbol{x}^{t+1}\right)-f\left(\boldsymbol{x}^{t}\right) \leq-\frac{1}{2 L}\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}^{2}.\]为了递归的表示 $f\left(\boldsymbol{x}^{t}\right)$,我们将 $\left|\nabla f\left(\boldsymbol{x}^{t}\right)\right|_{2}$ 替换为 $f\left(\boldsymbol{x}^{t}\right)$ 的函数。 为此,利用 convexity 得到
\[\begin{aligned} &f\left(\boldsymbol{x}^{*}\right)-f\left(\boldsymbol{x}^{t}\right) \geq \nabla f\left(\boldsymbol{x}^{t}\right)^{\top}\left(\boldsymbol{x}^{*}-\boldsymbol{x}^{t}\right) \geq-\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2}\left\|\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right\|_{2} \\ &\Longrightarrow \quad\left\|\nabla f\left(\boldsymbol{x}^{t}\right)\right\|_{2} \geq \frac{f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right)}{\left\|\boldsymbol{x}^{t}-\boldsymbol{x}^{*}\right\|_{2}} \ge \frac{f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right)}{\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}} \end{aligned}\]令
\[\Delta_{t} :=f\left(\boldsymbol{x}^{t}\right)-f\left(\boldsymbol{x}^{*}\right)\]可得 (代入Fact 2)
\[\Delta_{t+1}-\Delta_{t} \leq-\frac{1}{2 L\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}^{2}} \Delta_{t}^{2}\]下面用归纳法证明 $\Delta_{t} \leq \frac{b}{t} \quad$, 其中
\[b=2 L\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}^{2}.\]如果该不等式对 $t$ 成立,那么
\[\Delta_{t+1} \leq \Delta_{t}-\Delta_{t}^2/b.\]而这个不等式在 $\Delta_{t}<b/2$ 时增, 我们让
\[\Delta_{t} \leq \frac{b}{t}\le \frac{b}{2},\]那么函数始终对 $\Delta_{t}$ 是增的, 也就是当 $t\ge 2$ 时函数对 $\Delta_{t}$ 增。 因此有
\[\Delta_{t+1} \leq \frac{b(t-1)}{t^{2}} \leq \frac{b}{t+1}. \blacksquare\]
非凸问题 Nonconvex problems
许多代价函数都是非凸的,比如低秩矩阵补全,盲逆卷积,字典学习,混合模型,深度神经网络学习……对于这样的函数,可能到处都有 bumps 和 局部最小值。没有算法可保证有效解决所有情况的非凸问题。
典型的收敛保证
我们很难希望快速收敛到全局最优解,但是我们或许可以有
- 收敛到驻点
- 收敛到局部最小
- 局部收敛到全局最小(需要合适的初始化)
如果我们只希望找到一个(近似的)驻点 $\epsilon$-approximate stationary point,那么我们的目标就是找到点 $x$ 使得
\[\|\nabla f(\boldsymbol{x})\|_{2} \leq \varepsilon\]GD 可以达到这个目标吗?
Theorem 7 Let $f$ be $L$-smooth and $\eta_{k} \equiv \eta=1 / L$. Assume $t$ is even.
-
in general, GD obeys
\[\min _{0 \leq k<t}\left\|\nabla f\left(\boldsymbol{x}^{k}\right)\right\|_{2} \leq \sqrt{\frac{2 L\left(f\left(\boldsymbol{x}^{0}\right)-f\left(\boldsymbol{x}^{*}\right)\right)}{t}}\] -
if $f$ is convex, then GD obeys
\[\min _{t / 2 \leq k<t}\left\|\nabla f\left(\boldsymbol{x}^{k}\right)\right\|_{2} \leq \frac{4 L\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}}{t}\]
GD 找 $\epsilon$-approximate stationary point 需要 $O\left(1 / \varepsilon^{2}\right)$ 次迭代。并不意味着 GD 收敛到驻点,只是说在 GD 的轨迹中存在一个$\epsilon$-approximate stationary point.
证明: 由 Fact 2 有 $\frac{1}{2 L}\left|\nabla f\left(\boldsymbol{x}^{k}\right)\right|_{2}^{2} \leq f\left(\boldsymbol{x}^{k}\right)-f\left(\boldsymbol{x}^{k+1}\right), \; \forall k$, 那么
\[\begin{aligned} \frac{1}{2 L} \sum_{k=t_{0}}^{t-1}\left\|\nabla f\left(\boldsymbol{x}^{k}\right)\right\|_{2}^{2} & \leq \sum_{k=t_{0}}^{t-1}\left(f\left(\boldsymbol{x}^{k}\right)-f\left(\boldsymbol{x}^{k+1}\right)\right)=f\left(\boldsymbol{x}^{t_{0}}\right)-f\left(\boldsymbol{x}^{t}\right) \\ & \leq f\left(\boldsymbol{x}^{t_{0}}\right)-f\left(\boldsymbol{x}^{*}\right) \\ \Longrightarrow \quad \min _{t_{0} \leq k<t}\left\|\nabla f\left(\boldsymbol{x}^{k}\right)\right\|_{2} & \leq \sqrt{\frac{2 L\left(f\left(\boldsymbol{x}^{t_{0}}\right)-f\left(\boldsymbol{x}^{*}\right)\right)}{t-t_{0}}} \end{aligned}\]对于一般情况,令 $t_{0}=0$ 即可得证。 如果 $f$ convex, 由 Theorem 6
\[f\left(\boldsymbol{x}^{t_{0}}\right)-f\left(\boldsymbol{x}^{*}\right) \leq \frac{2 L\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}^{2}}{t_{0}}\]令 $t_{0}=t / 2$ 可得
\[\min _{t_{0} \leq k<t}\left\|\nabla f\left(\boldsymbol{x}^{k}\right)\right\|_{2} \leq \frac{2 L}{\sqrt{t_{0}\left(t-t_{0}\right)}}\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}=\frac{4 L\left\|\boldsymbol{x}^{0}-\boldsymbol{x}^{*}\right\|_{2}}{t}\]逃离鞍点 Escaping saddles
至少有两种点梯度为0,一种是全局/局部最小,另一种是鞍点。鞍点看上去是不稳定的 critical points,我们有办法逃离鞍点吗?
GD 有时候确实逃离不了鞍点,比如 $x^0$ 恰好是鞍点,那么 GD 就陷入其中。但好在当随机初始化 random initialization 时这种情况通常可以被避免。 幸运的是,在温和条件下,随机初始化的 GD 几乎都能收敛到局部(有时甚至是全局)最优解。
References
[1] Chen, Yuxin, Lecture Notes: Gradient methods for unconstrained problems, 2018.
[2] Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Science & Business Media, 2009.