Artificial Intelligence by MIT 2

大纲

• Modeling Problem Solving
  • Generating Test
  • Problem Reduction
• Problem Reduction Tree
• Transforms + Examples
• Reflections

总结

• Knowledge about knowledge is power
• Catechism
  • What kind
  • How represented
  • How used
  • How much
  • What exactly

实例：积分问题

我们不能一眼看出积分的解，但是可以编程求解该问题。这样的程序是智能的嘛？

程序在解复杂积分问题的时候，方法和人类解是一样的嘛？是的。举求解该问题的例子，很麻烦 grungy，但仍然要做，因为：

什么是 education philosophy? want to have a skill –> need to understand –> need to witness low level things (examples, details)

我们再解一个复杂积分问题时，通常将之简化为另一个积分问题，称为“Problem Reduction”. 整个过程可以画成一个 problem tree， 也称 AND/OR tree，Goal Tree.

这通常涉及到转化，首先我们希望转化是尽可能 safe 的。首先列出一定正确的最安全的积分法则（它们的本质是 knowledge），然后试着将它们用到我们的求解积分的程序中。

• 负号可以提到积分外面
• 常因子可以提到积分外面
• 和的积分等于积分的和
• 分子阶数大于分母阶数的有理式必须约分

Apply all safe tranformation –> Look at the table –> Done? 要注意的是，又一个问题转化成的未必是一个问题，可能是若干小的问题。这时就产生了“与”结点。同时，转化的方法可能不唯一，因此就有了“或”结点。

但是，这些 Safe Transforms 有时不足以解决问题。这时我们要引入 Heuristic Transforms.

• 三角变换，所有的三角函数可以写成 cos x 和 sin x 的函数。
• tan x 的函数可以写成 y 的函数除以 $(1+y^{2})$.
• $1-x^{2}$ –> x = sin y; $1+x^{2}$ –> x = tan y.

当面对“或”结点时，该作何选择呢？选择最简单的那个。如何衡量简单与否？ 看因式分解的符号最少的那个方法。

由于安全方法转化没有风险，而策略方法转化可能有风险，因此每一次转化后我们总是先检查是否可以直接由安全方法解决该问题。这样，就形成了下面的循环。

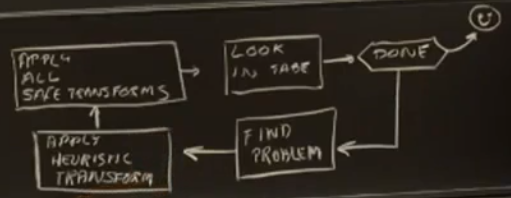
Reflection

出错往往是检查程序的好时机。

树最深的深度是多少？平均深度又是多少？旁支大概有多少？ 借此可以对该问题的本质有更好的了解。

上面这个程序需要用到哪些知识呢？积分变换的知识，目标树原理的知识，何时无需变换直接查表。

知识是如何表达的呢？ 知识最终是用列表来表示的。

尾声

现在回过头来看最开始的问题，这个程序具有智能嘛？ Well，当我们不知道它如何运作的时候，我们看到它的表现，会觉得了不起；一旦我们知道它的工作原理，我们就不再觉得它智能了——原来如此，并没有什么神奇之处嘛。